The apparent depth of the dot from outside of the three immiscible liquids is

Given:

The densities of the liquid are given in order of and refractive indices are. The height of the beaker is denoted as h and height of each immiscible liquid is Apparent height of the three liquid are given as. The refractive index of air is

Formula Used:

To find the apparent depth of the dot for a near normal vision, we use the ratio of apparent depth and real depth to the ratio of refractive indices of liquids.

where

is the apparent depth of the liquid and is the real depth of the liquid, is the refractive index of the viewer and is the refractive index of the object which is to be viewed is placed.

Explanation:

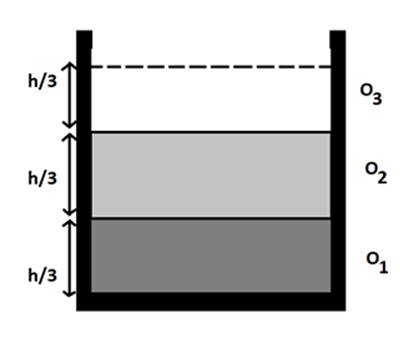
As mentioned above the apparent depths are given as.

Therefore, the when seeing the dot from the apparent depth is

The apparent depth of when viewing from

The apparent depth of, when viewed from the outer surface or air

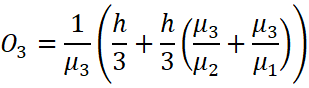
Therefore, the apparent depth from the outside of the three immiscible liquid is