A circular disc of radius ‘R’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’ (Fig. 9.5). The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index μ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?
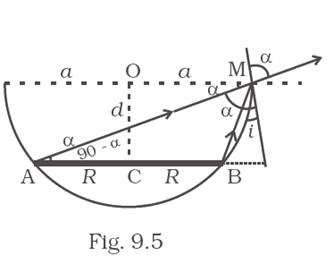
The disc from the top of the bowl is placed at a distance of ![]() .
.
Given:
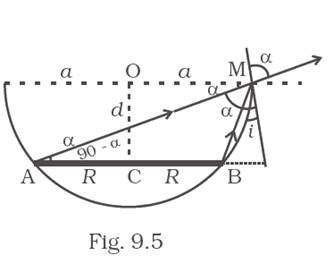
The radius of the circular disc is R, the radius of the bowl is a, and the refractive index of the liquid is ![]() , to find the distance of the disc from the top we use the relationship of refractive index and sine values of incidence and refractive angles. The refractive angle r =
, to find the distance of the disc from the top we use the relationship of refractive index and sine values of incidence and refractive angles. The refractive angle r =![]() .
.
Formula used:
The formula used to find the distance is Snell’s Law. Snell’s Law is the ratio of sine value of incidence angle and refractive angle equivalent to the refractive incidence of the medium on which the light ray falls, in this case the refractive index of the transparent liquid.
![]()
where
i is the angle of incidence, and r is the refractive angle and ![]() is the refractive index of the transparent liquid.
is the refractive index of the transparent liquid.
Explanation:
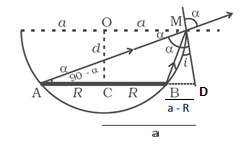
According to the Snell’s Law the value of the refractive index of the liquid is
![]()
To find the value of![]() , let us take the triangle MBD
, let us take the triangle MBD
![]()
Height = BD and Hypotenuse = MB
![]()
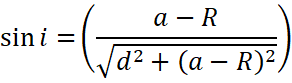
To find the value of![]() , let us take the triangle AMD
, let us take the triangle AMD
Height = AD and Hypotenuse = MA
![]()
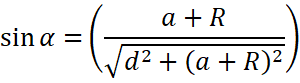
Putting the value of ![]() and
and ![]() and
and ![]() respectively in Snell’s Law
respectively in Snell’s Law
Due to opposite refraction the formula in such cases is reciprocal of refractive index.
![]()
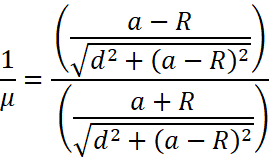
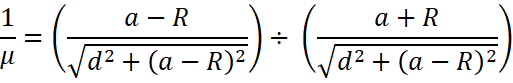
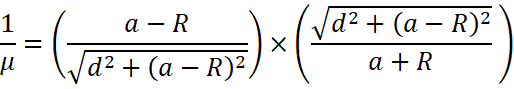
Squaring both the sides we get
![]()
![]()
![]()
![]()
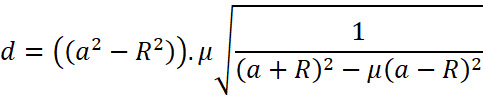
Therefore, the distance of the disc from the top i.e. the value of the d is![]() .
.