A jar of height h is filled with a transparent liquid of refractive index μ (Fig. 9.6). At the center of the jar on the bottom surface is a dot. Find the minimum diameter of a disc, such that when placed on the top surface symmetrically about the center, the dot is invisible.

Question

Philoid · Accepted Answer

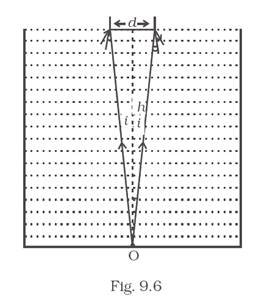
The minimum diameter of the disc to render the dot at the bottom of the jar invisible is.

Given:

The height of the jar is given as h, to find the minimum diameter of the disc to render the dot at bottom invisible we need to find relation between the depth of the dot placed, critical angle and the refractive index of the liquid.

Formula Used:

Critical angle of incidence, is the angle which when formed in a denser medium turns the refracted angle into .

where

is the refractive index of the denser medium and c is the critical angle.

Explanation:

In the figure below when the light ray strikes the bottom of the jar at the dot it refracts basically in three directions, when the light reflects in case of ray 1 it refracts to rarer medium angle less than the crtical angle, when refracts at critical angle c it pass parallel to the medium just as in case 2 and when the light refracts in case 3 it falls back to the denser medium thus doesn’t refracts in the rarer medium.

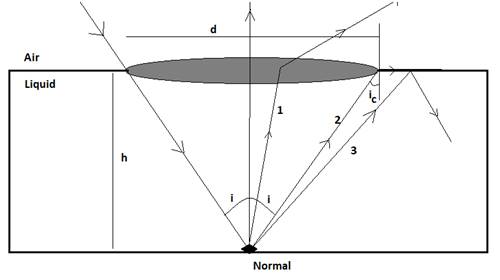
Finding the critical angle in terms of h and d

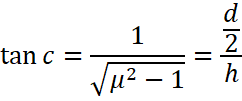
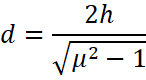
Therefore, the minimum diameter of the disc to render the dot at the bottom of the jar invisible is.