The ray travels along the length of the medium MC, when the value of the sine is maximum and angle “a” is minimum.

Given:

The refractive index of the material is. To show that the light refracted is parallel to the medium of the surface by showing relationship between angle of incidence, refraction and refractive index of the material.

Formula used:

Snell’s law states the relationship between the sine values of incidence, refractive angles and refractive index of the material.

where

i is the angle of incidence, and r is the refractive angle and is the refractive index of the material. is the refractive index of the air

Explanation:

The path of refraction at critical angle is MC

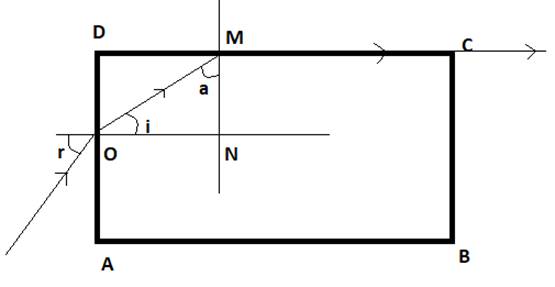
For reflection to stay on the path MC

From triangle MNO

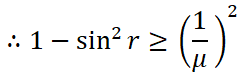
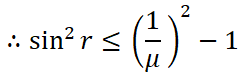
Using Snell’s law, we get

Squaring both the sides we get

When the value of angle of incidence is maximum then angle of refraction is maximum and the value of angle of a is minimum.

Let us take the value of i to be maximum that is

Therefore, it is proved that if refractive index is , then ray of light travels along the length perpendicular to the incidence.