The mixture a pure liquid and a solution in a long vertical column (i.e., horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d << h, the height of the column.
The angle of deviation is 
Given:
The vertical height of the column is much larger than the horizontal height. The width of the column = d, and the height of the column = h. using the relationship between the incidence and refraction with refractive index of the liquid to find the height of the column.
Formula Used:
Snell’s Law, is the ratio between the sine value of incidence and refraction with the ratio of refractive index of the mediums through which the light passes.
where
is the refractive index of the medium, 
is the refractive index of the air
. i is the angle of incidence and r is the angle of refraction.
Explanation:
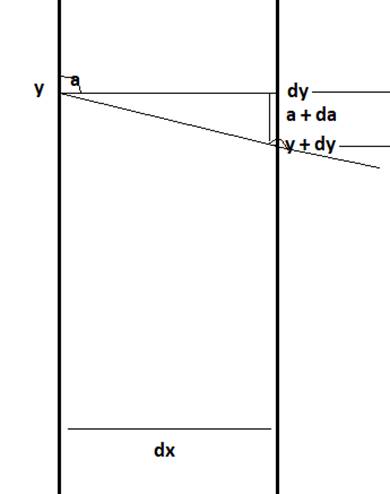
When the ray of light passes from x to dx inside the liquid, the angle of incidence of light at x is a, which passes through the tube at a height of y and is released at an angle of refraction at a + da, at a height of y + dy. Using snell’s law we get:
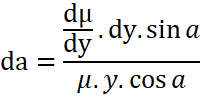
Putting 
Integrating both sides with second side from 
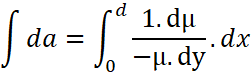
Therefore, the deviation in travelling a horizontal distance d << h, is
.