(i) Consider a thin lens placed between a source (S) and an observer (O) (Fig. 9.8). Let the thickness of the lens vary as where b is the vertical distance from the pole. w₀ is a constant. Using Fermat’s principle i.e. the time of transit for a ray between the source and observer is an extremum; find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.

Question

(i) Consider a thin lens placed between a source (S) and an observer (O) (Fig. 9.8). Let the thickness of the lens vary as where b is the vertical distance from the pole. w 0 is a constant. Using Fermat’s principle i.e. the time of transit for a ray between the source and observer is an extremum; find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length. (ii) A gravitational lens may be assumed to have a varying width of the form b min < b < b max b < b min Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius

Philoid · Accepted Answer

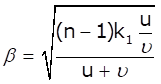
(i) The focal length of the lens is D

(ii) It is proved that that an observer will see an image of a point object as a ring about the center of the lens with an angular radius.

Given:

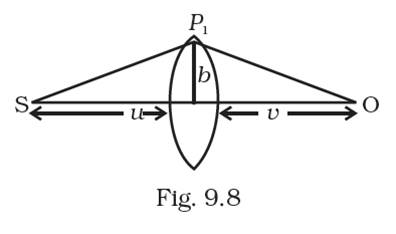
The thickness of the lens varies as. The vertical distance of the pole is b; to find the focal length of the lens in least amount of time taken by light ray to travel from incidence to refraction. The object distance from the lens is given as u and the image distance is v, the height of lens from the principal axis is b.

Formula used:

Fermat’s principle, this principal states the minimum amount of time taken to travel from one medium to another; Fermat’s principle is used to derive the Snell’s law and law of reflection.

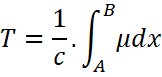
where

C denotes the speed of light that is, is the refractive index and dx is the infinitely small distance. Whereas A and B are the point of light entry and exit respectively. T is the time period required by light to travel from A to B.

Explanation:

Time required for light to travel from S to according to the diagram,

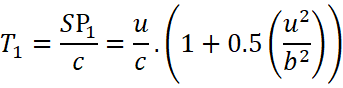
Time required for light to travel from to O

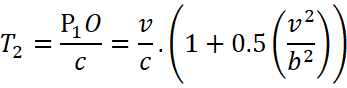
Time required traveling the thickness of the lens

The total time taken

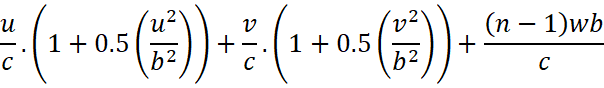
Putting the value of in 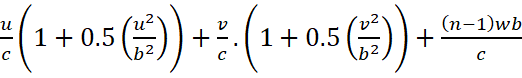we get

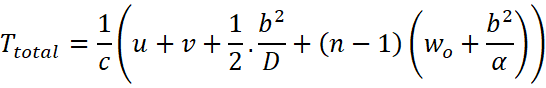
The formula for converging lens is

Therefore, the focal length of the lens is, with D is the focal length.

(ii) The total time taken

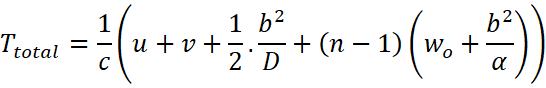
Differentiating both sides with respect to the length of the lens above the principal axis:

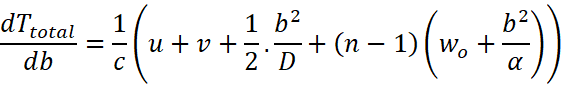
Putting the value of D = in

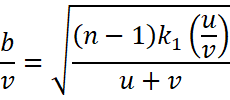
The value of

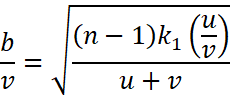
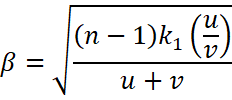
Therefore, it shows that an observer will see an image of a point object as a ring about the center of the lens with an angular radius.