For an LCR circuit driven at frequency ω, the equation reads
![]()
(i) Multiply the equation by i and simplify where possible.
(ii) Interpret each term physically.
(iii) Cast the equation in the form of a conservation of energy statement.
(iv) Integrate the equation over one cycle to find that the phase difference between v and i must be acute.
Given:
Equation given : ![]()
(i)
Multiplying the equation by I,![]()
Multiplying by (1/2) and substituting i=dq/dt![]()
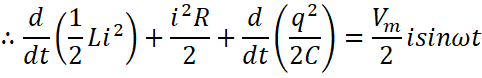
Hence, the simplified equation.
(ii)
Here, first term: ![]() means the rate of change of energy stored in the inductor.
means the rate of change of energy stored in the inductor.
Second term : ![]() represents the Joule’s Heating Loss.
represents the Joule’s Heating Loss.
Third Term: ![]() Represents rate of change of energy in Capacitor.
Represents rate of change of energy in Capacitor.
Fourth term: ![]() represents the energy due to driving force. It increases stored energy in inductor and capacitor.
represents the energy due to driving force. It increases stored energy in inductor and capacitor.
(iii)
Conservation of Energy states that:
The sum of the individual energies across the individual components is equal to the total power of the circuit.
The equation in the form of a conservation of energy statement is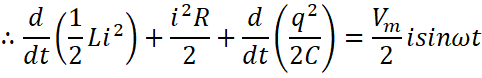
(iv)
Integrating the equation from 0 to T with resected to dt.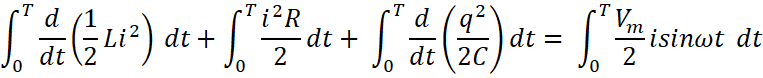
The integral of first term and third term would be zero as d/dt and dt gets cancelled. and V=Vmsinωt![]()
![]()
LHS is positive as i, R and T are always positive, hence RHS is also positive.
Hence, phase difference between v and I must be acute for the cycle to be positive.