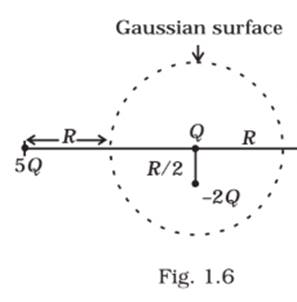
Refer to the arrangement of charges in Fig. 1.6 and a Gaussian surface of radius R with Q at the centre. Then
We know from Gauss Law that the closed surface integral of electric flux (![]() ) is equal to the charge enclosed (
) is equal to the charge enclosed (![]() ) by that closed surface. This is mathematically given by
) by that closed surface. This is mathematically given by
![]()
![]() The electric flux is given by
The electric flux is given by
![]()
The charge enclosed by the given Gaussian surface S shown in the figure below is given by
![]()
The ![]() do not include charge
do not include charge ![]() since it is outside the given Gaussian surface.
since it is outside the given Gaussian surface.
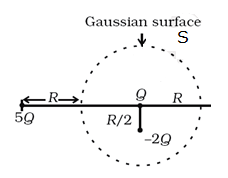
Therefore, using expression (2), the electric flux through the surface of given Gaussian surface is given by
![]()
Hence, the electric flux through the given Gaussian surface S is due to charges ![]() and
and ![]() only. So, the electric flux through the given Gaussian surface S due to charge
only. So, the electric flux through the given Gaussian surface S due to charge ![]() is zero.
is zero.
Therefore, option A and C are correct. The electric field on the given Gaussian surface is due to all charges present in the given figure and s given by
![]()