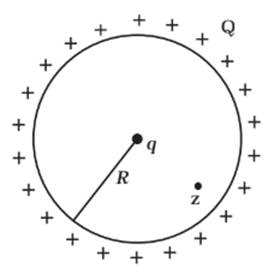
Ring is positively charged. If a positive charge is placed at the centre of the ring, it will experience a force in every direction as shown in the figure. So it remains at rest at the centre of the ring. If it is displaced away from the centre in the plane of ring, it will experience a force that will push it towards the centre. This equilibrium state is called as unstable equilibrium state.

Therefore, options A and D are correct.

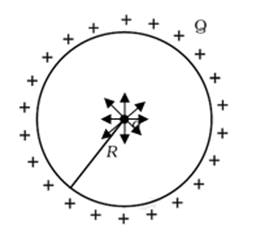
When a negative charge is displaced away from the centre in the plane of the ring, it will experience an attractive force and it will move until it hits the ring. Therefore, option B is also correct.

The electric field due to the positively charged ring is along the axis AB in positive x direction of the ring shown below.

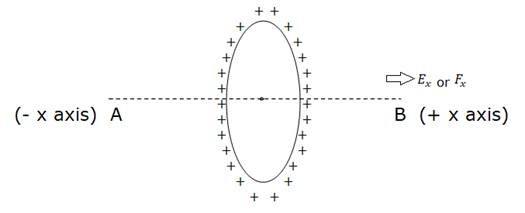
The electric field E_x is directly proportional to the distance between the plane of the ring and the point where electric field is to be determined. That is

Where q is the positive test charge

In the plane of the ring,

Equation (2) says that there is no force or electric field at the centre of the ring independent of any charged particle.

If now a negatively charged particle is displaced infinitesimally from the centre of the ring towards the +x direction along x-axis, the force on it, will be

Therefore, the force on negatively charged particle is in negative x direction. This particle thus gains some acceleration due to this force and hence the negatively charged particle moves past the centre of the ring towards the other side. Now, the charge is in -x direction and therefore the force will be

Therefore, the force on negatively charged particle now is in positive x direction.

This process continues and the charge moves to and fro along the axis. Thus, we say that the particle performs Simple Harmonic Motion (SHM) along the x axis shown below.

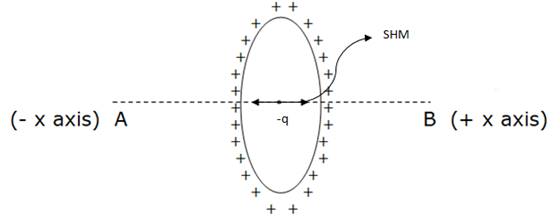
Therefore, option C is also correct.