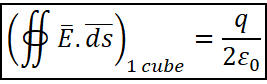What will be the total flux through the faces of the cube (Fig. 1.9) with side of length a if a charge q is placed at
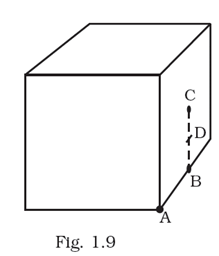
(a) A: a corner of the cube.
(b) B: mid-point of an edge of the cube.
(c) C: centre of a face of the cube.
(d) D: mid-point of B and C.
We know from Gauss Law that the closed surface integral of electric flux (![]() ) is equal to the charge enclosed (
) is equal to the charge enclosed (![]() ) by that closed surface. This is mathematically given by
) by that closed surface. This is mathematically given by
![]()
![]() The electric flux is given by
The electric flux is given by
![]()
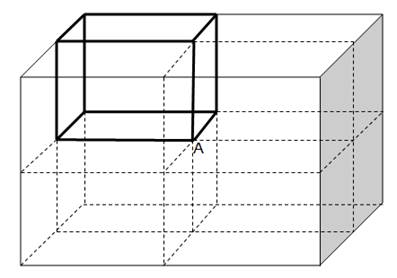
(a) Charge q is placed at point A corner of the cube of the given cube. To determine the flux through the faces of the given cube, we have to first consider a Gaussian surface. This surface must be a closed surface (here a large cube made up of 8 equivalent cubes) around the charge q at point A as shown in the figure below.
Using equation (2) above, the electric flux through the Gaussian surface is
![]()
But, we have to determine the flux through one cube (bolded in the figure below). Since the flux is ![]() contributed by 8 cubes (or large cube), the flux contributed by 1 cube will be
contributed by 8 cubes (or large cube), the flux contributed by 1 cube will be
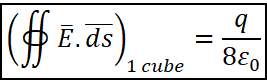
(b) Charge q is placed at point B which is at the midpoint of an edge of cube. To determine the flux through the faces of the given cube, we have to first consider a Gaussian surface. This surface must be a closed surface (here a large cube made up of 4 equivalent cubes) around the charge q at point B as shown in the figure below.
Using equation (2) above, the electric flux through the Gaussian surface is
![]()
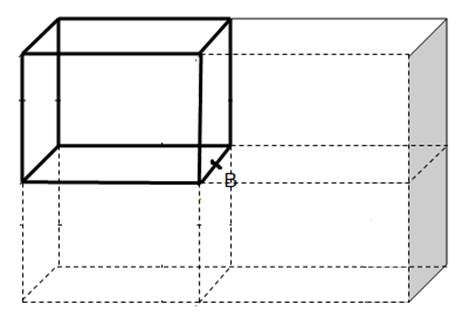
But, we have to determine the flux through one cube (bolded in the figure above). Since the flux is ![]() contributed by 4 cubes (or large cube), the flux contributed by 1 cube will be
contributed by 4 cubes (or large cube), the flux contributed by 1 cube will be
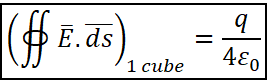
(c) Charge q is at point C which is at the centre of the face of a cube. To determine the flux through the faces of the given cube, we have to first consider a Gaussian surface. This surface must be a closed surface (here a large cube made up of 2 equivalent cubes) around the charge q at point C as shown in the figure below.
Using equation (2) above, the electric flux through the Gaussian surface is
![]()
But, we have to determine the flux through one cube (bolded in the figure below). Since the flux is ![]() contributed by 2 cubes (or large cube), the flux contributed by 1 cube will be
contributed by 2 cubes (or large cube), the flux contributed by 1 cube will be
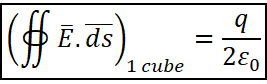
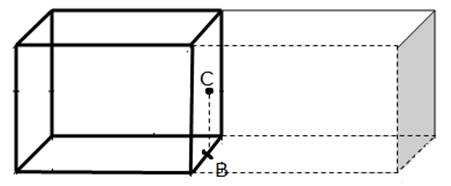
(d) Charge q is at point D which is at the centre of the line joining B and C on the face of a cube. To determine the flux through the faces of the given cube, we have to first consider a Gaussian surface. This surface must be a closed surface (here a large cube made up of 2 equivalent cubes) around the charge q at point D as shown in the figure below.
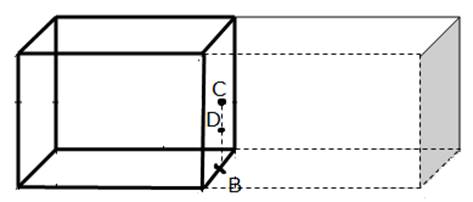
Using equation (2) above, the electric flux through the Gaussian surface is
![]()
But, we have to determine the flux through one cube (bolded in the figure below). Since the flux is ![]() contributed by 2 cubes (or large cube), the flux contributed by 1 cube will be
contributed by 2 cubes (or large cube), the flux contributed by 1 cube will be