In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.

(a) Find the critical value of y such that expansion may start.


(b) Show that the velocity of expansion is proportional to the distance from the Centre.


a) As given in question we have to assume that universe constituent is hydrogen and further we are assuming that universe is perfect sphere.


Keeping in the mind that fundamental forces like electrostatic forces and gravitation will be the deciding factors.


As we know that hydrogen contains one e- and one p+


So we can get the charge on one hydrogen atom and that is


qH= ep + e- = -(1+y)e + e = -ye


Or magnitude wise |ye|


We know the integral form of gauss theorem which is



Here,


E=electric field


ds=small area


Q=charge enclosed


= permittivity of free space or vacuum


Number density = N


∴ Total charge will be


Since the universe is considered to be spherical,



∴


∴


So Electrostatic force on a hydrogen atom at distance R will be E × ye


i.e.


as it will be repulsive in nature


Coming to gravitational field


We know that the mass of an atom of hydrogen is equal to mass of proton let it be mP


Total mass of hydrogen atom


We know gravitational field





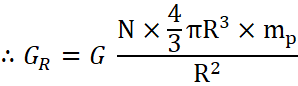
The –ive sign suggests it is attractive in nature


So for expansion of world electrostatic force should be greater than gravitational force


i.e.


For minimum case ,


Where G = 6.674×10-11 Nm2 kg-2


And


mp = 1.6726219 × 10-27 kilograms



Solving this we get


b) So now net force experienced by hydrogen atoms is





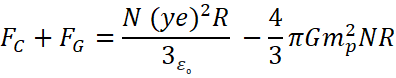
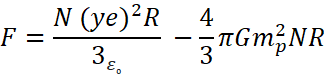
As we know,





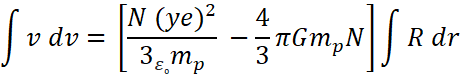
Let, (since it is a constant term)




Where R is position from center.


1