Consider a sphere of radius R with charge density distributed as ρ(r) = kr for r ≤ R = 0 for r R . a) Find the electric field at all points r. (b) Suppose the total charge on the sphere is 2e where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero. Assume that the introduction of the proton does not alter the negative charge distribution.

Question

Consider a sphere of radius R with charge density distributed as ρ(r) = kr for r ≤ R = 0 for r >R . a) Find the electric field at all points r. (b) Suppose the total charge on the sphere is 2e where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero. Assume that the introduction of the proton does not alter the negative charge distribution.

Philoid · Accepted Answer

For E for r ≤ R

We know the integral form of gauss theorem which is

As the electric field vector and surface area vector are ⊥as shown in

fig 1.27 b

∴

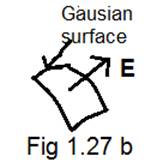
For ,

Let, dv be a small volume component,

Since the gaussian surface is spherical,

⇒

⇒k

As shown in fig 1.27 a Gaussian surface is inside the actual sphere

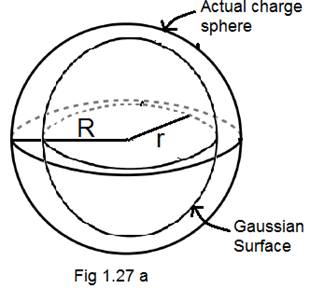
∴ for r≤ R

Now for r >R.

Gaussian surface will be outside the actual sphere

And Q_enc will be fixed

Now,

for r >R .

b) The two protons should be kept at equal distance from the Centre of sphere so that the attractive force on both of them is same. As depicted in the fig 1.27 c

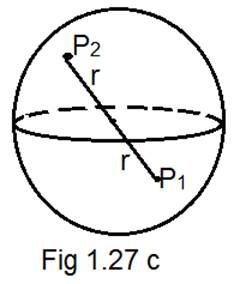
Charge on the sphere; As found in previous part.

And according to question i.e = 2e

∴

Now as we can see there will be two type of forces on a proton, one attractive force due to negative charge distribution on sphere and repulsive due to other proton.

∴One attractive force due to negative charge distribution on sphere;

; as we found for r ≤ R

F_attractive -----eq.1

Substituting the value of k in eq.1

We get F attractive

And repulsive due to other proton.

By applying coulombs law i.e. k

So, F repulsive

Or, F repulsive

∴ Net force on proton will be zero if F attractive + F repulsive =0

∴
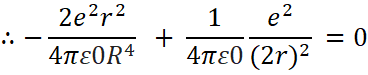