Two fixed, identical conducting plates (α &β) , each of surface area S are charged to –Q and q, respectively, where Q > q > 0. A third identical plate (
), free to move is located on the other side of the plate with charge q at a distance d (Fig 1.13). The third plate is released and collides with the plate β. Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst 
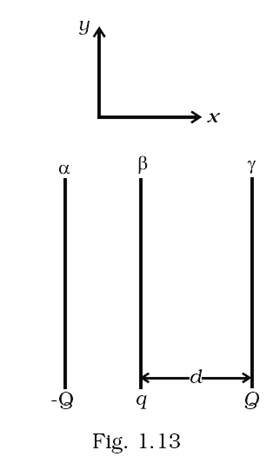
(a) Find the electric field acting on the plate 
before collision.
(b) Find the charges on β and 
after the collision.
(c) Find the velocity of the plate 
after the collision and at a distance d from the plate β.
a)
We know that Electric field due to infinite plate is given by 
Where
Surface charge density
i.e
where A is surface area
∴The electric field on 
=
i.e towards left
and the electric field on 
=
i.e towards right
∴ Net electric field on 
b) During collision plate 
are in contact, so they must be at same potential
Let suppose charge on 
is q1 after collision and charge q2 on 
after collision
There should be a point o where the E must be 0,
∴ E on point O 
=
i.e towards left
∴ E on point O 
= 
towards right
∴ E on point O 
= 
to the left
As At point O E = 0
∴
= 
i.eq2 
----Eq. 1
According to principle of conservation of charge there should be no loss of charge due to collision
∴ 
----- Eq. 2
Solving eq. 1 and eq. 2 we get
q1 (charge on 
) 
charge q2 on 
c)The work done on plate 
till it reaches 
W = F1d
F1 = E1Q
Where E1= Net electric field on 
by 
and 
i.e
∴ 
And after collision E due to 
=
∴
= 
Total Work done = (F1+F2)d
= 
[Using work energy theorem,which states that the work done by all forces acting on a particle equals the change in the particle’s kinetic energy.
]
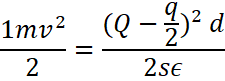
