Total charge –Q is uniformly spread along length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring. (a) Show that the particle executes a simple harmonic oscillation. (b) Obtain its time period.

Question

Philoid · Accepted Answer

a)

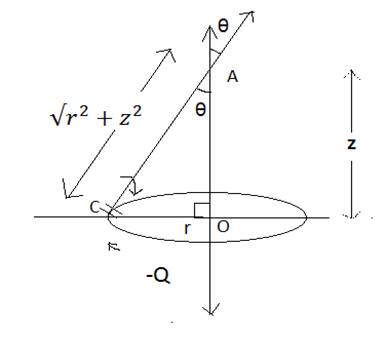
Due to a small element of the ring on the z-axis the effective field will be

.cosθeq .1

In triangle AOC,

( By Pythagoras Theorem)

Now,

eq .2

Equating 1 and 2

= eq.3

=

Integrating above equation we get,

=

Since, -Q charge is uniformly distributed over the ring,

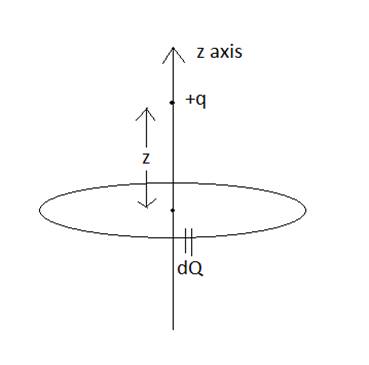
According to question +q is displaced by z distance along the centre of the ring at the axis of ring. So,

Force on +q charge will be,

F= eq.4

But as z<<<1 and <<<1

F=

Using binomial expansion,

,where x<<1

So,

F= eq.5

Since is very small the term in the bracket can be taken as 1. Therefore equation 5 becomes,

F= eq.6

From simple harmonic motion(SHM) we know that a particle to follow a simple harmonic motion it should follow the relation

a –x

where x=displacement from mean position and

a=- eq.7

and =

so comparing the force equation as we obtained in the equation 6 with equation 7 we get,

=

∴

b) As we know

∴T=

Total charge –Q is uniformly spread along length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.(a) Show that the particle executes a simple harmonic oscillation.(b) Obtain its time period.

Total charge –Q is uniformly spread along length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.
(a) Show that the particle executes a simple harmonic oscillation.

(b) Obtain its time period.