If and are two triangles such that , then Area ( ): Area ( ) =

Question

Philoid · Accepted Answer

Given ΔABC and ΔDEF are two triangles such that

We know that if two triangles are similar then their sides are proportional.

Since , ΔABC and ΔDEF are similar.

We know that the ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

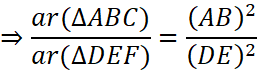
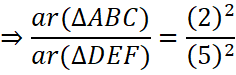
∴ ar (ΔABC): ar (ΔDEF) = 4: 25