The left block in figure (12-E13) moves at a speed u towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that the motions of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.

Question

Philoid · Accepted Answer

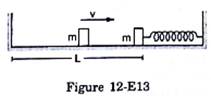
When the block A moves with the velocity v and collides with the block B, it transfers all energy to the block B (elastic collision). The block A will move a distance x against a spring, again the block B will return to the original point and completes half of the oscillations.

So, the time period of B is

The block collides with the block A and comes to rest at that point. The block A moves a further distance

L to return to its original position.

Therefore, time taken by the block to move from M→N and N→M is

Hence time period of the periodic motion is