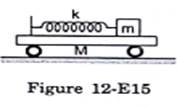
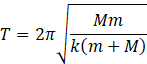All the surfaces shown in figure (12-E15) are frictionless. The mass of the car is M, that of the block is m and the spring has spring constant k. Initially, the car and the block are at rest and the spring is stretched through a length x when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the car as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
Let the amplitude of oscillation of m and M be ![]() respectively.
respectively.
a) From law of conservation of momentum
![]()
Again
![]()
![]()
From above equations
![]()
![]()
![]()
b) At any position, let the velocities be ![]()
Here ![]() is the velocity of m with respect to M. Hence following the energy method that total energy should be constant.
is the velocity of m with respect to M. Hence following the energy method that total energy should be constant.
![]()
Again from law of conservation of momentum,
![]()
![]()
Putting the above values in equation A we get,
![]()
![]()
Taking the time derivative of above equation on both sides, we get
![]()
![]()
![]()
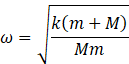
Therefore, time period is given by