A small block oscillates back and forth on a smooth concave surface of radius R (figure 12-E17). Find the time period of small oscillation.
Given radius of the concave surface = R
Let mass of the block be ‘m’
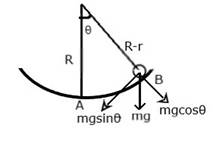
Driving force F = mgsinθ
Therefore a= gsinθ
a
gθ →1 [for small angles sinθ 
]
if x is the displacement of block from mean postion then sinθ =x/R
θ 
x/R [for small angles sinθ 
]
substituting in eqn 1 a = gx/R →2
from SHM equation a = 
x →3
comparing 2 and 3 we get ω = 
Time period T =
= 2π 
1