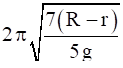
given,

Radius of the surfaces = R

Radius of the ball = r

Mass of the ball = m

Let angular amplitude be

Torque on the ball

Moment of inertia of ball

( for spherical surface)

(parallel axis theorem)

Angular acceleration of a ball

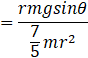
Angular acceleration about the center of the surface

(effective distance R-r)

(for smaller angles )

Linear acceleration