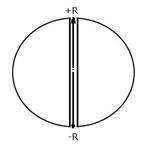
Assume that a tunnel is dug across the earth (radius =R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of √gR (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of √gR.
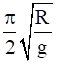 in each case
in each case
a) Here we need to calculate the time period of the oscillation of a particle and center of the earth acts as mean position.
Let position of particle = ![]()
Velocity = ![]()
Acceleration = ![]()
![]() Time period
Time period ![]()
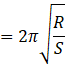
Velocity ![]() [ Let ‘A’ be the amplitude ]
[ Let ‘A’ be the amplitude ]
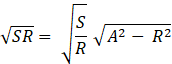
![]()
![]()
![]()
![]()
Let ![]() be the time when particle is at distance ‘R’
be the time when particle is at distance ‘R’
From equation ![]()
![]()
![]()
![]()
![]()
Let ![]() be the time when particle is at distance ‘-R’
be the time when particle is at distance ‘-R’
![]()
![]()
![]()
![]()
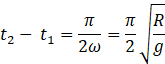
b) when body is dropped from a height ‘R’. the final velocity of the body on reaching the ground is ‘v’
we know ![]()
![]()
![]()
We know ![]()
![]()
![]()
This is same velocity as in case (a). therefore time taken to cover the length of tunnel will be same
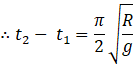
c) when it is projected upwards with velocity ![]() it reaches the surface with the same velocity
it reaches the surface with the same velocity ![]() .
.
From there it enters tunnel with same velocity as in case (a) and hence time taken to cover the tunnel will be ![]()