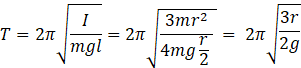Find the time period of small oscillations of the following systems. (a) A metre stick suspended through the 20 cm mark. (b) A ring of mass m and radius r suspended through a point on its periphery. (e) A uniform square plate of edge a suspended through a corner. (d) A uniform disc of mass m and radius r suspended through a point r/2 away from the centre.

(a) 1.51 s


(b)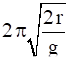


(c)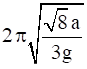


(d)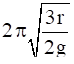


(a) time period for a physical pendulum is given by


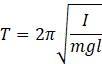
where’l’ is the distance between centre of mass and point of suspension








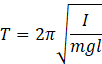
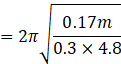
= 1.51 sec


(b)




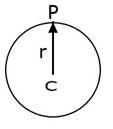
when a ring is suspended through a point on its periphery,




[]



 here l= r




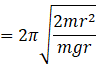
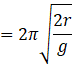
(c)



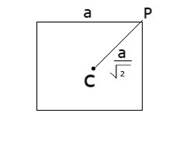
when axis pass through corner of the square , we should consider moment of inertia in two directions






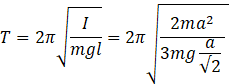
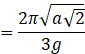
(d) uniform disc of a mass m and radius r suspended through a point r/2 away from center


Given l=r/2




=



1