A uniform disc of radius r is to be suspended through a small hole made in the disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?
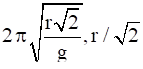
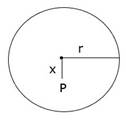
Let x be the distance between centre of mass and point of suspension ‘P’
I = 
=
We have T 
=
= 
= 
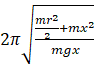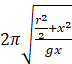The condition for minimum of T is 
= 
= 2π× (1/2) 
(
)=0
Consider (
) term , (
)=0
x= r/
minimum possible time period is at x = r/
= 
1