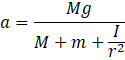Figure (10-E4) shows two blocks of masses m and M connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotate about this axis. Find the acceleration of the mass M assuming that the string does not slip on the pulley.
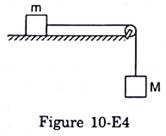
The acceleration of the mass M is 
Given
The blocks are of “m” and “M” masses, with radius of r pulley and moment of Inertia “I”
Formula Used
The formula used to find the acceleration of the mass pulled/pushed is determined by the second law of Newton when the Force/Tension applied is equivalent to the product of mass and acceleration
where
is the force of the mass in terms of tension, 
is the acceleration and m is the mass of the block.
Explanation
The diagram 10.E4.1 is drawn below for better understanding of the kinematics of the blocks
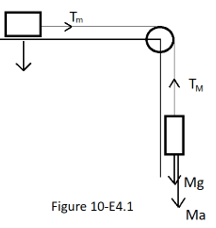
The tension applied on the first block is
The tension applied on the block of mass “m” is
The torque applied on the pulley is derived as
The angular acceleration is changed into normal linear acceleration.
