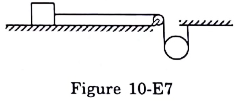
The descending pulley shown in figure (10-E7) has a radius 20 cm and moment of inertia 0.20 kg-m2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1.0 kg.
The acceleration of the mass if 1 kg is ![]()
Given
The blocks are of “m” and “M” masses, with radius of r pulley and moment of Inertia “I”
Formula Used
The formula used to find the acceleration of the mass pulled/pushed is determined by the second law of Newton when the Force/Tension applied is equivalent to the product of mass and acceleration
![]()
where
![]() is the force of the mass in terms of tension,
is the force of the mass in terms of tension, ![]() is the acceleration and m is the mass of the block.
is the acceleration and m is the mass of the block.
Explanation
The diagram 10-E7.1 as drawn below shows the tension horizontal as T’ and tension pulling the pulley as T which gives us the diagram as
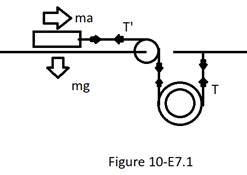
The tension in terms of acceleration due to horizontal tension is
![]()
![]()
The angular acceleration of the pulley is given as
![]()
Hence, the torque applied by the pulley due to the mass is given as
![]()
![]()
![]()
![]()
Now finding the moment of Inertia we get the value of the mass M as
![]()
![]()
Putting the value of mass in tension equation, we get the equation of acceleration in terms of tension as
![]()
Again, putting the value of ![]() , we get
, we get
![]()
![]()
![]()