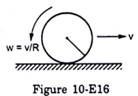
A solid sphere is set into motion on a rough horizontal surface with a linear speed u in the forward direction and an angular speed u/R in the anticlockwise direction as shown in figure (10-E 16). Find the linear speed of the sphere (a) when it stops rotating and (b) when slipping finally ceases and pure rolling starts.

Question

Philoid · Accepted Answer

Given:

Radius of the sphere= R

Linear velocity = u

Angular speed = u/R

Let us consider the point A, where external torque is zero

Using law of conservation of angular momentum

(b) linear speed when it starts rolling