A block of mass sliding on a smooth horizontal surface with a velocity 
meets a long horizontal spring fixed at one end and having spring constant k as shown in figure (8-E10). Find the maximum compression of the spring. Will the velocity of the block be the same as
when it comes back to the original position shown?
The compression distance of the spring is given as 
Given
The sliding velocity of the block is given as 
with spring constant k.
Formula Used
Using the conversation of energy, we equate the energies of spring compression and potential energy of the mass of the block, the formula of the energy stored in spring compression is
And the energy stored in the block is formulated as
where
The value of spring constant is denoted as “k”, the compression distance is “x”, the mass of the block is given as “m”, v is the velocity of the block.
Explanation
The kinetic energy of the block is given as
The energy stored in the compressed spring is given as
Equating the energies together we get the compression distance as
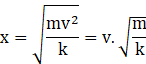
The compression distance of the spring is given as 