A chain of length l and mass m lies on the surface of a smooth sphere of radius R >l with one end tied to the top of the sphere.
(a) Find the gravitational potential energy of the chain with reference level at the centre of the sphere. (b) Suppose the chain is released and slides down the sphere. Find the kinetic energy of the chain, when it has slid through an angle θ.
(c) Find the tangential acceleration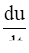 
of the chain when the chain starts sliding down.
The gravitational potential energy of the chain is 
The chain is released and slides down the sphere
The tangential acceleration of the chain is
Given
The length of the chain is l, mass of the chain is m, and the radius of the sphere is given as R.
Formula Used
The formula for the total energy in terms of kinetic and potential energy is given as
where
The 
is the total energy in terms of kinetic and potential energy, m is the mass of the object, g is the acceleration in terms of gravity and l is the length of the object, 
is the angle of exit.
Explanation
(a) Let the angle formed by the chain is = 
The length of the chain = 
Therefore, the angle is written as 
The length of the chain in terms of radius is 
The force derivative of the chain is given as 
The potential energy is calculated as 
The P.E. after integration is
(b) The kinetic energy and the potential energy of the chain is equivalent to
The initial potential energy is calculated as
The change in the potential energy is
.
(c) Now to find the tangential velocity we use the equation of
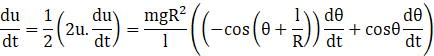
After reduction the value of the 
is
