(a) Define a wavefront.
(b) Using Huygens’ principle, draw the diagrams to show the nature of the wavefronts when an incident plane wavefront gets
(i)reflected from a concave mirror,
(ii)refracted from a convex lens.
(c) Draw a diagram showing the propagation of a plane wavefront from denser to a rarer medium and verify Snell’s law of refraction.
OR
(a)A concave mirror produces a real and magnified image of an object kept in front of it. Draw a ray diagram to show the image formation and use it to derive the mirror equation.
(b)A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12 cm from P. At what point does the beam converge if the lens is
(i)a convex lens of focal length 20 cm,
(ii)a concave lens of focal length 16 cm?
(a) A wave-front is defined as the locus of all points in a wave surface having a constant phase or same phase.
(b) Huygens principle states that every point in a wave-front is a source of secondary wavelet.
(i) The following diagram shows a wave-front reflected from a concave mirror.
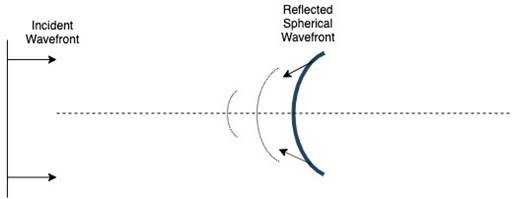
(ii) The following diagram shows a wave-front refracted from a convex lens.
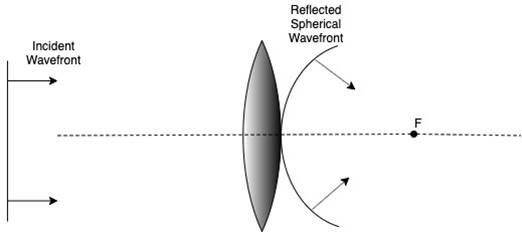
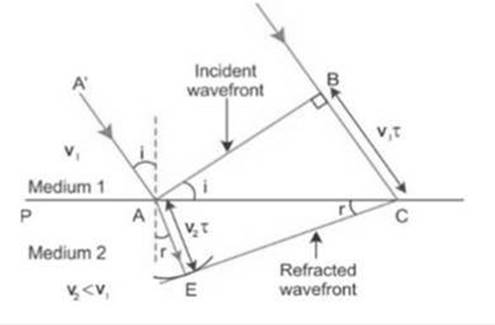
(c) The following diagram illustrates Snell’s law using Huygens principle.
In the figure, i is the angle of incidence, r is the angle of refraction.
Let the speed of light in two mediums be 
and 
. Let 
be the time taken by wavefront to travel distance BC.
Therefore, 
Now, we draw an arc of radius of length 
from A. Next we draw a tangent from C to the arc. Creating 
.
From the figure,
In 
, 
In 
, 
Therefore, 
Now, we know that the refractive index relates to the velocities as
Therefore, 
and 
Hence,
Thus, Huygens principle can be used to prove Snell’s law of reflection.
OR
(a) The following diagram illustrates the image formation by a concave mirror.
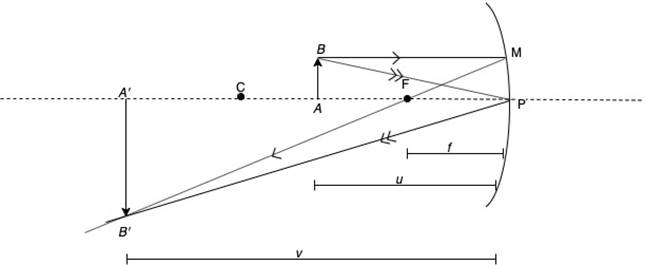
As evident from the figure, 
and 
are similar.
Hence,
And 
and 
are similar.
From the figure, 
Here,
Dividing both sides with uvf and rearranging we get
Which is the mirror equation.
(b) We know, the lens equation is
where, v is the image distance, u the object distance and f is the focal length.
Here it is given that the image distance, 
. We need to find the image distance in both the cases.
(i) given, focal length, 
(ii) given, focal length, 
