A mass m = 50 g is dropped on a vertical spring of spring constant 500 N m-1 from a height h = 10 cm as shown in figure (18-E14). The mass sticks to the spring and executes simple harmonic oscillations after that. A concave mirror of focal length 12 cm facing the mass is fixed with its principal axis coinciding with the line of motion of the mass, its pole being at a distance of 30 cm from the free end of the spring. Find the length in which the image of the mass oscillates.
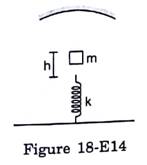
mass of the object, m= 50g
Spring constant of the spring, k= 500N/m
Height of mass from the spring, h= 10cm
Focal length of the mirror, f= 12cm
Distance between the pole and the free end of spring = 30cm
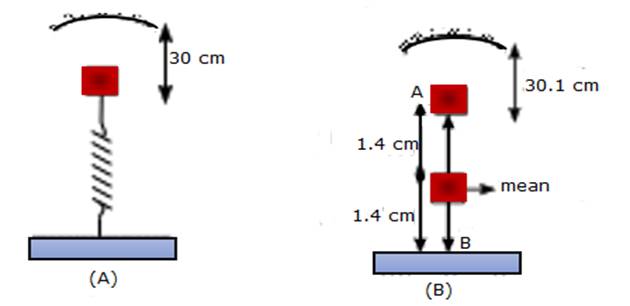
The spring execute SHM when mass falls on it
At equilibrium position, weight of mass is equal to force applied by the spring
![]()
![]()
![]()
Therefore, mean position of SHM = 30+ 0.1= 30.1 cm (from pole of the mirror)
Let the maximum compression =![]()
Using the work energy principle,
![]()
![]()
![]()
From the figure shown,
Position of point B= 30+1.5=31.5 cm (from the pole of the mirror)
Therefore, amplitude of vibration of SHM= 31.5-30.1= 1.4 cm
Position of the point A from the pole of the mirror= 30.1 – 1.4= 28.7 cm
For point A,
Object distance, ![]()
Using lens formula,
![]()
![]()
![]()
For point A,
Object distance, ![]()
Using lens formula,
![]()
![]()
![]()
the image vibrates in length (20.62 - 19.38) = 1.24 cm