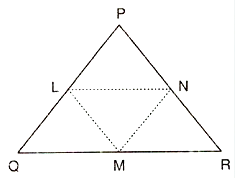
Given that in Δ PQR,

PQ = QR

And, L, M, N are the mid points of the sides PQ, QR and RP respectively.

We have to prove that,

LN = MN

Here, we can observe that PQR is an isosceles triangle

PQ = QR

And, ∠QPR = ∠QRP (i)

And also, L and M are the mid points of PQ and QR respectively

PL = LQ =

QM = MR =

And, PQ = QR

PL = LQ = QM = MR = = (ii)

Now, in

LP = MR (From ii)

∠LPN = ∠MRN (From i)

PN = NR (N is the mid-point of PR)

Hence, By SAS theorem

, LN = MN (By c.p.c.t)