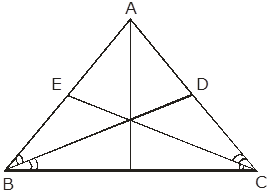
Given,

In isosceles Δ ABC,

BD and CE are bisectors of ∠B and ∠C

And,

AB = AC

To prove: BD = CE

Proof: In Δ BEC and Δ CDB, we have

∠B =∠C (Angles opposite to equal sides)

BC = BC (Common)

∠BCE = ∠CBD (Since, ∠C = ∠B ∠C = ∠B ∠BCE = ∠CBD)

By ASA theorem, we have

Δ BEC ≅ Δ CDB

EC = BD (By c.p.c.t)

Hence, proved