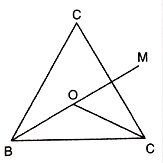
Given that in Δ ABC,

AB = AC and the bisectors of ∠B and ∠C intersect at O and M is a point on BO produced.

We have to prove ∠MOC = ∠ABC

Since,

AB = AC

Δ ABC is isosceles

∠B = ∠C

Or,

∠ABC = ∠ACB

Now,

BO and CO are bisectors of ∠ABC and ∠ACB respectively.

∠ABO = ∠OBC = ∠ACO = ∠OCB = ∠ABC = ∠ACB (i)

We have, in

∠OCB + ∠OBC + ∠BOC = 180^o (ii)

And also,

∠BOC + ∠COM = 180^o (iii) [Straight angle]

Equating (ii) and (iii), we get

∠OCB + ∠OBC + ∠BOC = ∠BOC + ∠COM

∠OBC + ∠OBC = ∠MOC

2∠OBC = ∠MOC

2(∠ABC) = ∠MOC [From (i)]

∠ABC = ∠MOC

Therefore, ∠MOC = ∠ABC