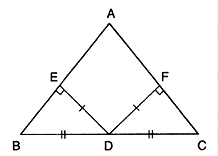
Given,

ABC is a triangle and D is the mid-point of BC

Perpendicular from D to AB and AC are equal.

To prove: Triangle is isosceles

Proof: Let DE and DF be perpendiculars from A on AB and AC respectively.

In order to prove that AB = AC, we will prove that Δ BDE ≅ Δ CDF.

In these two triangles, we have

∠BEF =∠CFD = 90°

BD = CD (Therefore, D is the mid-point of BC)

DE=DF (Given)

So, by RHS congruence criterion, we have

Δ BDE ≅ Δ CDF

∠B = ∠C (By c.p.c.t)

AC = AB (By c.p.c.t)

As opposite sides and opposite angles of the triangle are equal.

Therefore, Δ ABC is isosceles