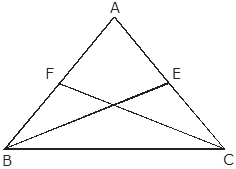
Given,

ABC is an isosceles triangle

AB = AC

BE and CF are two medians

To prove: BE = CF

Proof: In

CE = BF (Since, AC = AB = = AB = CE = BF)

∠ECB = ∠FBC (Angle opposite to equal sides are equal)

BC = BC (Common)

Therefore, By SAS theorem

BEC

(By c.p.c.t)