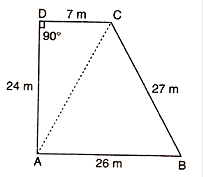
The sides of a quadrangular field, taken in order are 26 m, 27 m, 7 m, are 24 m respectively. The angle contained by the last two sides is a right angle. Find its area.
Let consider a quadrilateral ABCD
In ∆ADC;
AC = 
= 25 cm
In ∆ABC
AB = a = 26 cm, BC = b = 27 cm, AC = c = 25 cm
Let a, b and c are the sides of triangle and s is
the semi-perimeter, then its area is given by:
A = 
where 
= 
= 39
A1 = 
A1 = 
= 
cm2
In ∆ADC;
DA = a = 24 cm, CD = b = 7cm, AC = c = 25 cm
Let a, b and c are the sides of triangle and s is
the semi-perimeter, then its area is given by:
A = 
where 
[Heron’s Formula]
= 
= 28
A2 = 
A2 = 
= 
cm2
Therefore area of quadrilateral ABCD = A1 + A2 = 291.85+84 = 375.85 cm2
2