Book: RD Sharma - Mathematics
Chapter: 2. Polynomials
Subject: Maths - Class 10th
Q. No. 2 of Exercise 2.3
Listen NCERT Audio Books - Kitabein Ab Bolengi
Check whether the first polynomial is a factor of the second polynomial by applying the division algorithm:
(i) 
(ii)
(iii) 
(i) 
and 
Degree of 
; therefore degree of 
and degree of remainder is of degree 1 or less,
Let 
and 
By applying division algorithm:
Dividend = Quotient× Divisor + Remainder
On substituting values in the above relation we get,
On comparing coefficients we get,
On solving above equations we get,
, 
, 
, 
, 
On substituting these values for 
Since remainder is zero, therefore 
(ii) 
and 
Degree of 
; therefore degree of 
and degree of remainder is of degree 1 or less,
Let 
and 
By applying division algorithm:
Dividend = Quotient× Divisor + Remainder
On substituting values in the above relation we get,
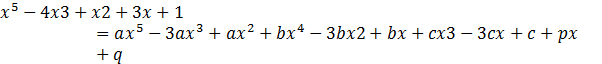
On comparing coefficients we get,
On solving above equations we get,
, 
, 
, 
, 
On substituting these values for 
Since remainder is 2, therefore 
(iii) 
and 
Degree of 
; therefore degree of 
and degree of remainder is of degree 2 or less,
Let 
and 
By applying division algorithm:
Dividend = Quotient× Divisor + Remainder
On substituting values in the above relation we get,
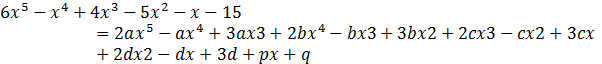
On comparing coefficients we get,
On solving above equations we get,
, 
, 
, 
, 
On substituting these values for 
Since remainder is 
, therefore 
, if two of its zeros are -2 and -1.
if one of its zeros is -2.
if two of its zeros are 
and 
.
it its two zeros are 
so that the resulting polynomial is exactly divisible by 
?
so that the resulting polynomial is exactly divisible by 
?
, if two of its zeros are 2 and-2.
, if two of its zeros are 
and 
.
, if two of its zeros are 
and 
.
, if two of its zeros are 
and 
.