(i) 8 as the sum

Total number of outcomes when a pair of die is thrown simultaneously is:

Here the first number denotes the outcome of first die and second number the outcome of second die.

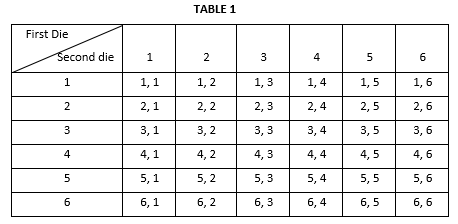
Total number of outcomes in the above table are 36

Numbers of outcomes having 8 as sum are: (6, 2), (5, 3), (4, 4), (3, 5) and (2, 6)

Therefore numbers of outcomes having 8 as sum are 5

Probability of getting numbers of outcomes having 8 as sum is =

Therefore Probability of getting numbers of outcomes having 8 as sum is

(ii) a doublet

Total number of outcomes in the above table 1 are 36

Numbers of outcomes as doublet are: (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) and (6, 6)

Therefore Numbers of outcomes as doublet are 6

Probability of getting numbers of outcomes as doublet is =

Therefore Probability of getting numbers of outcomes as doublet is

(iii) a doublet of prime numbers

Total number of outcomes in the above table 1 are 36

Numbers of outcomes as doublet of prime numbers are: (1, 1), (3, 3), (5, 5)

Therefore Numbers of outcomes as doublet of prime numbers are 3

Probability of getting numbers of outcomes as doublet of prime numbers is =

Therefore Probability of getting numbers of outcomes as doublet of prime numbers is

(iv) a doublet of odd numbers

Total number of outcomes in the above table 1 are 36

Numbers of outcomes as doublet of odd numbers are: (1, 1), (3, 3), (5, 5)

Therefore Numbers of outcomes as doublet of odd numbers are 3

Probability of getting numbers of outcomes as doublet of odd numbers is =

Therefore Probability of getting numbers of outcomes as doublet of odd numbers is

(v) a sum greater than 9

Total numbers of outcomes in the above table 1 are 36

Numbers of outcomes having sum greater than 9 are: (4, 6), (5, 5), (5, 6), (6, 6), (6, 4), (6, 5)

Therefore Numbers of outcomes having sum greater than 9 are 6

Probability of getting numbers of outcomes having sum greater than 9 is =

Therefore Probability of getting numbers of outcomes having sum greater than 9 is

(vi) An even number on first

Total numbers of outcomes in the above table 1 are 36

Numbers of outcomes having an even number on first are: (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5) and (6, 6)

Therefore Numbers of outcomes having an even number on first are 18

Probability of getting numbers of outcomes having An even number on first is =

Therefore Probability of getting numbers of outcomes having an even number on first is

(vii) an even number on one and a multiple of 3 on the other

Total numbers of outcomes in the above table 1 are 36

Numbers of outcomes having an even number on one and a multiple of 3 on the other are: (2, 3), (2, 6), (4, 3), (4, 6), (6, 3) and (6, 6)

Therefore Numbers of outcomes having an even number on one and a multiple of 3 on the other are 6

Probability of getting an even number on one and a multiple of 3 on the other is =

Therefore Probability of getting an even number on one and a multiple of 3 on the other is

(viii) neither 9 nor 11 as the sum of the numbers on the faces

Total numbers of outcomes in the above table 1 are 36

Numbers of outcomes having 9 nor 11 as the sum of the numbers on the faces are: (3, 6), (4, 5), (5, 4), (5, 6), (6, 3) and (6, 5)

Therefore Numbers of outcomes having neither 9 nor 11 as the sum of the numbers on the faces are 6

Probability of getting 9 nor 11 as the sum of the numbers on the faces is =

The probability of outcomes having 9 nor 11 as the sum of the numbers on the faces P(E) =

Probability of outcomes not having 9 nor 11 as the sum of the numbers on the faces is given by P() =

Therefore probability of outcomes not having 9 nor 11 as the sum of the numbers on the faces = P() =

Therefore Probability of getting neither 9 nor 11 as the sum of the numbers on the faces is

(ix) a sum less than 6

Total numbers of outcomes in the above table 1 are 36

Numbers of outcomes having a sum less than 6 are: (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)

Therefore Numbers of outcomes having a sum less than 6 are 10

Probability of getting a sum less than 6 is =

Therefore Probability of getting sum less than 6 is

(x) a sum less than 7

Total numbers of outcomes in the above table 1 are 36

Numbers of outcomes having a sum less than 7 are: (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (5, 1)

Therefore Numbers of outcomes having a sum less than 7 are 15

Probability of getting a sum less than 7 is =

Therefore Probability of getting sum less than 7 is

(xi) a sum more than 7

Total numbers of outcomes in the above table 1 are 36

Numbers of outcomes having a sum more than 7 are: (2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 3), (5, 4), (5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)

Therefore Numbers of outcomes having a sum more than 7 are 15

Probability of getting a sum more than 7 is =

Therefore Probability of getting sum more than 7 is

(xii) at least once

Total numbers of outcomes in the above table 1 are 36

Therefore Numbers of outcomes for atleast once are 11

Probability of getting outcomes for atleast once is =

Therefore Probability of getting outcomes for atleast once is

(xiii) a number other than 5 on any dice.

Total numbers of outcomes in the above table 1 are 36

Numbers of outcomes having 5 on any die are: (1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)

Therefore Numbers of outcomes having outcomes having 5 on any die are 15

Probability of getting 5 on any die is =

Therefore Probability of getting 5 on any die is

Probability of not getting 5 on any die P() = 1 –P (E)

P() =