In Fig. 10.61, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF (ii) radius of the circle.
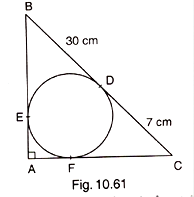
Given : AB, BC and AC are tangents to the circle at E, D and F.
BD = 30 cm and DC = 7 cm and ∠BAC = 90°
Recall that tangents drawn from an exterior point to a circle are equal in length
Hence BE = BD = 30 cm
Also FC = DC = 7 cm
Let AE = AF = x → (1)
Then AB = BE + AE = (30 + x)
AC = AF + FC = (7 + x)
BC = BD + DC = 30 + 7 = 37 cm
Consider right Δ ABC, by Pythagoras theorem we have
BC2 = AB2 + AC2
⇒ (37)2 = (30 + x)2 + (7 + x)2
⇒ 1369 = 900 + 60x + x2 + 49 + 14x + x2
⇒ 2x2 + 74x + 949 – 1369 = 0
⇒ 2x2+ 74x – 420 = 0
⇒ x2 + 37x – 210 = 0
⇒ x2 + 42x – 5x – 210 = 0
⇒ x (x + 42) – 5 (x + 42) = 0
⇒ (x – 5) (x + 42) = 0
⇒ (x – 5) = 0 or (x + 42) = 0
⇒ x = 5 or x = – 42
⇒ x = 5 [Since x cannot be negative]
∴ AF = 5 cm [From (1)]
Therefore AB =30 +x = 30 + 5 = 35 cm
AC = 7 + x = 7 + 5 = 12 cm
Let ‘O’ be the centre of the circle and ‘r’ the radius of the circle.
Join point O, F; points O, D and points O, E.
From the figure,
Area of (ΔABC) = Area (ΔAOB) + Area (ΔBOC) + Area (ΔAOC)![]()
∴ r = 5
Thus the radius of the circle is 5 cm