The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 meters towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use ![]() ).
).
Let the height of the tower = h (m)
In ∆ABC,
tan 30° = ![]()
![]() =
= ![]()
![]() =
= ![]()
√3h = 150+![]()
![]() -------- (1)
-------- (1)
In ∆ABD,
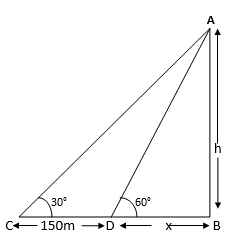
tan 60° = ![]()
√3 = ![]() ⇒ h = √3
⇒ h = √3 ![]()
![]() -------(2)
-------(2)
on substituting value of x from eqn.(2)i eqn.(1)
![]()
![]()
h-3h = -150![]()
2h = 150√3
h = ![]() ⇒ 75
⇒ 75![]()
h= 129.9 m.
Hence height of tower is 129.9 m.
14