From the top of a building 15 m high the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between the tower and building.
Let the distance between tower and building = ![]() (m)
(m)
In ∆ABC,
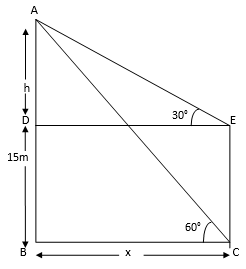
tan 60° = ![]()
√3 = ![]()
![]() =
= ![]()
√3 ![]() = h+15
= h+15
h = √3![]() -15 ------(1)
-15 ------(1)
In ∆ABE,
tan 30° = ![]()
![]()
![]() ---------(2)
---------(2)
![]()
![]()
h = 3h-15 ⇒ 2h = 15
h = ![]() ⇒ 7.5 m.
⇒ 7.5 m.
Height of tower = 15+7.5 ⇒ 22.5 m.
![]() ⇒ 12.99 m.
⇒ 12.99 m.
Therefore distance between tower and building is 12.99 m.
17