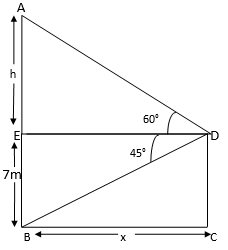
From the top a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Let the distance between the foots of building and cable tower is 
(m).
The height of cable tower = AB = AE+EB ⇒ (h+7)m.
In ∆AED,
tan 60° = 
√3 = 
h = √3 
---------(1)
The height of cable tower = AB = AE+EB ⇒ (h+7)m.
In ∆DEB,
tan 45° = 
1 = 
----------(2)
On substituting value of 
in eqn. (1)
h = 7√3
Height of cable tower is (h+7)m.
⇒ 7√3+7
⇒ 7(√3+1)m.
Therefore height of cable tower is 7(√3+1)m.
28