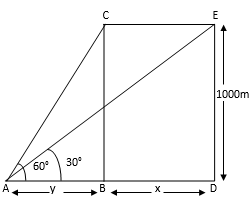
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km / hr.
In the fig let C be the initial position of the aeroplane. After 10 seconds the position of the aeroplane becomes E.
In ∆ABC
tan 60° = 
√3 = 
√3y = 1000m
y = 
-------(2)
In ∆ADE
tan 30° = 
= 
x + y = 1000√3
On substituting value of y from eqn (1)
x + 
= 1000√3
x = 1000-√3 - 
⇒ 
⇒ 
⇒ 
⇒ 1154.7m
Since the distance travelled by aeroplane in 10 seconds is 1154.7m. Therefore distance travelled by aeroplane in 1 hour =
⇒ 415.69 km/hr
Therefore speed of aeroplane is 415.69 km/hr
45