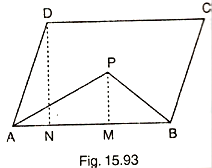
If P is any point in the interior of a parallelogram ABCD, then prove that area of the triangle APB is less than half the area of parallelogram.

Question

Philoid · Accepted Answer

Construction: Draw DN⊥ AB and PM⊥ AB.

Proof: Area of parallelogram ABCD = AB * DN

Area (Δ APB) = (AB * PM)

= AB * PM < AB * DN

= (AB * PM) < (AB * DN)

= Area (Δ APB) < Area of parallelogram ABCD