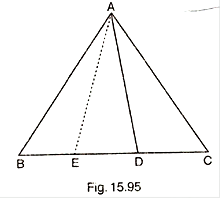
A point D is taken on the side BC of a Δ ABC such that BD = 2DC. Prove that

Question

A point D is taken on the side BC of a &#x394; ABC such that BD = 2DC. Prove that ar(&#x394; ABD) = 2ar(&#x394; ADC)

Philoid · Accepted Answer

Given that,

In Δ ABC,

We have

BD = 2DC

To prove: Area () = 2 Area ()

Construction: Take a point E on BD such that, BE = ED

Proof: Since,

BE = ED and,

BD = 2DC

Then,

BE = ED = DC

Median of the triangle divides it into two equal triangles

Since,

AE and AD are the medians of ΔABD and AEC respectively

Therefore,

Area (ΔABD) = 2 Area (ΔAED) (i)

And,

Area (ΔADC) = Area (ΔAED) (ii)

Comparing (i) and (ii), we get

Area (ΔABD) = 2 Area (ΔADC)

Hence, proved