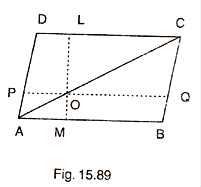
In Fig. 15.89, ABCD is a || gm . O is any point on AC. PQ||AB and LM||AD. Prove that: ar(|| gm DLOP) = ar(|| gm BMOQ)

Question

Philoid · Accepted Answer

Since,

A diagonal of parallelogram divides it into two triangles of equal area

Therefore,

Area ( = Area ()

Area ( + Area of parallelogram DLOP + Area ()

Area ( + Area of parallelogram DLOP + Area ( (i)

Since,

AO and CO are diagonals of parallelograms AMOP and OQCL respectively

Therefore,

Area ( = Area ( (ii)

Area ( = Area ( (iii)

Subtracting (ii) from (iii), we get

Area of parallelogram DLOP = Area of parallelogram BMOQ.