In Fig. 15.91, ABC is a right triangle right angled at A, BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX⊥ DE meets BC at Y. Show that:
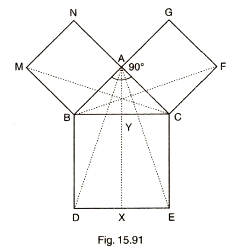
(i) Δ MBC ≅ ABD (ii) ar(BYXD) =2ar(Δ MBC)
(iii) ar(BYXD) = ar(ABMN)
(iv) Δ FCB ≅ Δ ACE
(v) ar(CYXE) = 2ar(Δ FCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = ar(ABMN)+ ar(ACFG)
(i) In ![]() , we have
, we have
MB = AB
BC = BD
And,
∠ MBC = ∠ ABD (Therefore, ∠MBC and ∠ABC are obtained by adding ∠ABC to right angle)
So, by SAS congruence rule, we have
![]()
Area (![]() ) = Area (
) = Area (![]() (1)
(1)
(ii) Clearly, ![]() and rectangle BYXD are on the same base BD and between the same parallels AX and BD
and rectangle BYXD are on the same base BD and between the same parallels AX and BD
Therefore,
Area (![]() =
= ![]() Area of rectangle BYXD
Area of rectangle BYXD
Area of rectangle BYXD = 2 Area (![]() )
)
Area of rectangle BYXD = 2 Area (![]() ) (2)
) (2)
[Therefore, Area (![]() = Area (
= Area (![]() ] From (1)
] From (1)
(iii) Since,
![]() and square MBAN are on the same base MB and between the same parallel MB and NC
and square MBAN are on the same base MB and between the same parallel MB and NC
Therefore,
2 Area (![]() ) = Area of square MBAN (3)
) = Area of square MBAN (3)
From (2) and (3), we have
Area of square MBAN = Area of rectangle BXYD
(iv) In ![]() , we have
, we have
FC = AC
CB = CE
And,
∠FCB = ∠ACE (Therefore, ∠FCB and ∠ACE are obtained by adding ∠ACB to a right angle)
So, by SAS congruence rule, we have
![]()
(v) We have,
![]()
Area (![]() Area (
Area (![]()
Clearly,
![]() and rectangle CYXE are on the same base CE and between the same parallel CE and AX
and rectangle CYXE are on the same base CE and between the same parallel CE and AX
Therefore,
2 Area (![]() = Area of rectangle CYXE
= Area of rectangle CYXE
2 Area (![]() = Area of rectangle CYXE (4)
= Area of rectangle CYXE (4)
(vi) Clearly,
![]() and rectangle FCAG are on the same base FC and between the same parallels FC and BG
and rectangle FCAG are on the same base FC and between the same parallels FC and BG
Therefore,
2 Area (![]() = Area of rectangle FCAG (5)
= Area of rectangle FCAG (5)
From (4) and (5), we get
Area of rectangle CYXE = Area of rectangle ACFG
(vii) Applying Pythagoras theorem in ![]() , we have
, we have
BC2 = AB2 + AC2
BC * BD = AB * MB + AC * FC
Area of rectangle BCED = Area of rectangle ABMN + Area of rectangle ACFG