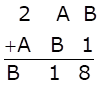
Here, in unit’s place,

B + 1 = 8

∴ B = 7

Now in ten’s place,

A + B = 1

∴ A + 7 = 1

∴ A = -6 which is not possible.

Hence, A + B > 9

Now, we carry one in hundred’s place and hence subtract 10 from ten’s place

∴ In ten’s place,

A + B – 10 = 1

∴ A + 7 = 11

∴ A = 4

Now to check whether our values of A and B are correct, we solve for hundred’s place.

2 + A + 1 =B

RHS = 2 + 4 + 1 = 7 = B =LHS

Hence, A = 4 and B = 7