Let us consider a triangle ABC in which CD ⊥ AB

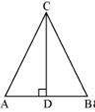
It is given that

Cos A = Cos B

In Δ ADC, cos A = AD/AC

In Δ ADB, cos B = BD/BC

⇒ AD/AC = BD/BC ..(i)

We have to prove ∠A = ∠B. To prove this, let us extend AC to P such that BC = CP, as shown below:

Now, From equation (i), we obtain

⇒ AD/AC = BD/BC .

Rewriting we get, (BC = CP)

⇒ AD/AC = BD/CP ..(i)

Now, if we join, B and P to get BP, as shown, below:

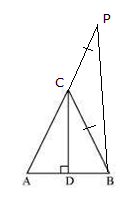
Then, by using the converse of Basic proportionality theorem we get,

Now, CD||BP

⇒ ∠ACD = ∠CPB (Corresponding angles) ..(iii)

⇒ ∠BCD = ∠CBP (Alternate interior angles) ...(iv)

And, by construction, we have BC = CP

∠CBP = ∠CPB (Angle opposite to equal sides of a triangle) ...(v)

From equations (iii), (iv), and (v), we obtain

∠ACD = ∠BCD ..Eq. (vi)

Now, In ΔCAD and ΔCBD,

∠ACD = ∠BCD [Using equation equation (vi)]

∠CDA = ∠CDB (Both 90°)

Therefore, the remaining angles should be equal

⇒ ∠CAD = ∠CBD

⇒ ∠A = ∠B