State whether the following are true or false. Justify your answer.

(i) The value of tan A is always less than 1


(ii) Secfor some value of angle A


(iii) Cos A is the abbreviation used for the cosecant of angle A


(iv) Cot A is the product of cot and A.


(v) for some angle θ

(i) Consider a ΔABC, right-angled at B


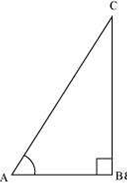
Tan A =


But > 1


Tan A > 1


So, Tan A < 1 is not always true


Hence, the given statement is false


(ii) Sec A =




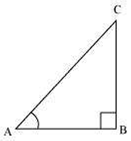
Let AC be 12k, AB will be 5k, where k is a positive integer


Applying Pythagoras theorem in ΔABC, we obtain


AC2 = AB2 + BC2


(12k)2 = (5k)2 + BC2


144k2 = 25k2 + BC2


BC2 = 119k2


BC = 10.9k


It can be observed that for given two sides AC = 12k and AB = 5k,


BC should be such that,


AC - AB < BC < AC + AB


12k - 5k < BC < 12k + 5k


7k < BC < 17 k


However, BC = 10.9k. Clearly, such a triangle is possible and hence, such value of sec A is possible


Hence, the given statement is true


(iii) Abbreviation used for cosecant of angle A is cosec A. And Cos A is the abbreviation used for cosine of angle A


Hence, the given statement is false


(iv) Cot A is not the product of cot and A. It is the cotangent of ∠A


Hence, the given statement is false


(v) sin θ =


In a right-angled triangle, hypotenuse is always greater than the remaining two sides. Therefore, such value of sin θ is not possible


Hence, the given statement is false


23