Book: NCERT - Mathematics
Chapter: 8. Introduction to Trigonometry
Subject: Maths - Class 10th
Q. No. 5 of Exercise 8.4
Listen NCERT Audio Books - Kitabein Ab Bolengi
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
(i) 
(ii) 
(iii) 
(iv) 
(v) 
using the identity 
(vi) 
(vii) 
(viii)
(ix) 
[Hint: Simplify LHS and RHS separately]
(x) 
(i) 
LHS = (cosec θ - cot θ)
= (
– 
)2
= 
= (1 - cos θ)2/sin2 θ
= (1 – cos θ)2/1 – cos2 θ
= (1 – c0s θ)2/ (1 – cos θ) (1 + cos θ)
= 
= RHS
(ii) 
LHS = 
+ 
= cos2A + (1 + sin2A)/(1 + sinA) (cos A)
= cos2A + 1 + sin2A + 2sinA/(1 + sinA) (cosA)
= sin2A + cos2A + 1 + 2sinA/(1 + sinA) (cosA)
= 
= 
= 
= 
= 2 sec A
= RHS
(iii) 
[Hint: Write the expression in terms of sin θ and Cos θ]
= 
= 
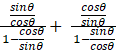
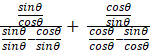
= sin2 θ/[cos θ (sin θ – cos θ)] + cos2 θ/ [sin θ (cos θ – sin θ)]
= sin2 θ/[cos θ (sin θ - cos θ)] – cos2 θ/[sin θ (sin θ - cos θ)]
= 1/(sin θ - cos θ) [(sin2 θ/cos θ) – (cos2 θ/sin θ)]
= 1/(sin θ – cos θ) * [(sin 3 θ – cos3 θ)/sin θ cos θ]
= [(sin θ – cos θ) (sin2 θ + cos2 θ + sin θcos θ)]/ [sin θ - cos θ) sin θ cos θ]
= (1 + sin θ cos θ)/sin θ cos θ
= 1/sin θ cos θ + 1
= 1 + sec θ cosec θ
= RHS
(iv) 
[Hint: Simplify LHS and RHS separately]
LHS = (1 + secA)/ secA
= (1 + 1/cos A)/1/cos A
= (cos A + 1)/cosA/1/cosA
= cos A + 1
RHS = sin2A/(1 – cos A)
= (1 – cos2A)/(1 – cos A)
= (1 – cos A) (1 + cos A)/ (1 – cos A)
= cos A + 1
LHS = RHS
(v) 
using the identity 
LHS = (cos A – sin A + 1)/ (cos A + sin A – 1)
Dividing Numerator and Denominator by sin A
= (c0s A – sin A + 1) / sin A/ (cos A sin A – 1) / sin A
= (cot A – 1 + cosec A)/ (cot A + 1 – cosec A)
= (cot A – cosec2A + cot2A + cosec A)/ (cot A + 1- cosec A) [Using cosec2A – cot2A = 1]
= [(cot A + cosec A) – (cosec A + cot A) (cosec A – cot A)]/ (1 – cosec A + cot A)
= (cot A + cosec A) (1 – cosec A + cot A)/ (1 – cosec A + cot A)
= cot A + cosec A
= RHS
(vi) 
Dividing numerator and denominator of LHS by cos A
= 
= 
= 
* 
= [(sec A + tan A)2/sec2A – tan2A]1/2
= 
= sec A + tan A
= RHS
(vii) 
(sin θ – 2 sin3 θ)/ (2cos3 θ – cos θ)
= [sin θ (1 – 2sin2 θ)]/[cos θ (2cos2 θ – 1)]
= sin θ [1 – 2 (1 – cos2 θ)] / [cos θ (2 cos2 θ – 1)]
= [sin θ (2cos2 θ – 1)] / [cos θ (2cos2 θ – 1)]
= tan θ = RHS
(viii)
LHS = (sin A + cosec A)2 + (cos A + sec A)2
= (sin2A + cosec2A + 2sin A cosec A) + (cos2A + sec2A + 2 cos A sec A)
= (sin2A + cos2A) + 2 sin A (1/sinA) + 2cos A (1/cosA) + 1 + tan2A + 1 + cot2A
= 1 + 2 + 2 + 2 + tan2A + cot2A
= 7 + tan2A + cot2A
= RHS
(ix) 
[Hint: Simplify LHS and RHS separately]
LHS = (cosec A – sin A) (sec A – cos A)
= (1/sin A – sin A) (1/cos A – cos A)
= [(1 – sin2A)/ sinA] [(1 – cos2A)/cosA]
= (cos2A/sin A) * (sin2A/cos A)
= cos A sin A
RHS = 1/(tan A + cot A)
= 1 / (sin A/cos A + cos A / sin A)
= 1/[(sin2A + cos2A)/sin A cos A]
= cos A sin A
LHS = RHS
(x) 
LHS = (1 + tan2A/ 1 + cot2A)
= (1 + tan2A / 1 + 1/tan2A)
= 1 + tan2A/ [(1 + tan2A)/tan2A]
= tan2A
